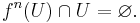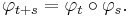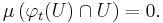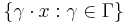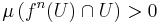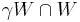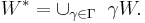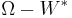Wandering set
In those branches of mathematics called dynamical systems and ergodic theory, the concept of a wandering set formalizes a certain idea of movement and mixing in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system. This is very much the opposite of a conservative system, for which the ideas of the Poincaré recurrence theorem apply. Intuitively, the connection between wandering sets and dissipation is easily understood: if a portion of the phase space "wanders away" during normal time-evolution of the system, and is never visited again, then the system is dissipative. The language of wandering sets can be used to give a precise, mathematical definition to the concept of a dissipative system. The notion of wandering sets in phase space was introduced by Birkhoff in 1927.
Contents |
Wandering points
A common, discrete-time definition of wandering sets starts with a map 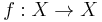 of a topological space X. A point
of a topological space X. A point 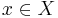 is said to be a wandering point if there is a neighbourhood U of x and a positive integer N such that for all
is said to be a wandering point if there is a neighbourhood U of x and a positive integer N such that for all  , the iterated map is non-intersecting:
, the iterated map is non-intersecting:
A handier definition requires only that the intersection have measure zero. To be precise, the definition requires that X be a measure space, i.e. part of a triple 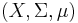 of Borel sets
of Borel sets  and a measure
and a measure  such that
such that
Similarly, a continuous-time system will have a map 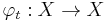 defining the time evolution or flow of the system, with the time-evolution operator
defining the time evolution or flow of the system, with the time-evolution operator  being a one-parameter continuous abelian group action on X:
being a one-parameter continuous abelian group action on X:
In such a case, a wandering point 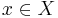 will have a neighbourhood U of x and a time T such that for all times
will have a neighbourhood U of x and a time T such that for all times 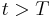 , the time-evolved map is of measure zero:
, the time-evolved map is of measure zero:
These simpler definitions may be fully generalized to a general group action. Let 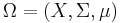 be a measure space, that is, a set with a measure defined on its Borel subsets. Let
be a measure space, that is, a set with a measure defined on its Borel subsets. Let  be a group acting on that set. Given a point
be a group acting on that set. Given a point 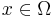 , the set
, the set
is called the trajectory or orbit of the point x.
An element 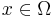 is called a wandering point if there exists a neighborhood U of x and a neighborhood V of the identity in
is called a wandering point if there exists a neighborhood U of x and a neighborhood V of the identity in  such that
such that
for all 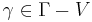 .
.
Non-wandering points
The definition for a non-wandering point is in a sense the converse. In the discrete case, 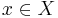 is non-wandering if, for every open set U containing x, one has that
is non-wandering if, for every open set U containing x, one has that
for some 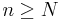 and any
and any 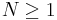 arbitrarily large. Similar definitions follow for the continuous-time and discrete and continuous group actions.
arbitrarily large. Similar definitions follow for the continuous-time and discrete and continuous group actions.
Wandering sets and dissipative systems
A wandering set is a collection of wandering points. More precisely, a subset W of  is a wandering set under the action of a discrete group
is a wandering set under the action of a discrete group  if W is measurable and if, for any
if W is measurable and if, for any 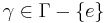 the intersection
the intersection
is a set of measure zero.
The concept of a wandering set is in a sense dual to the ideas expressed in the Poincaré recurrence theorem. If there exists a wandering set of positive measure, then the action of  is said to be dissipative, and the dynamical system
is said to be dissipative, and the dynamical system 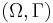 is said to be a dissipative system. If there is no such wandering set, the action is said to be conservative, and the system is a conservative system. For example, any system for which the Poincaré recurrence theorem holds cannot have, by definition, a wandering set of positive measure; and is thus an example of a conservative system.
is said to be a dissipative system. If there is no such wandering set, the action is said to be conservative, and the system is a conservative system. For example, any system for which the Poincaré recurrence theorem holds cannot have, by definition, a wandering set of positive measure; and is thus an example of a conservative system.
Define the trajectory of a wandering set W as
The action of  is said to be completely dissipative if there exists a wandering set W of positive measure, such that the orbit
is said to be completely dissipative if there exists a wandering set W of positive measure, such that the orbit 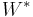 is almost-everywhere equal to
is almost-everywhere equal to  , that is, if
, that is, if
is a set of measure zero.
See also
References
- Nicholls, Peter J. (1989). The Ergodic Theory of Discrete Groups. Cambridge: Cambridge University Press. ISBN 0-521-37674-2.